の記事を書いてから、先行事例の調査が足りていなかったなと反省。 Latent Seed の Gaussian noise 間での morphing はあんまりやっている人いないんじゃないかな、と書いたけど、検索してみると普通に居た。
why settle for a few images from #stablediffusion when you can slowly walk your way around the sample space and create hyponotic videos you can't look away from? In this 2min video (~1hr to render on A100) I'm smoothly interpolating between random noise inputs into the model. pic.twitter.com/A4Ue1pqoMo
— Andrej Karpathy (@karpathy) August 16, 2022
Stable Diffusion が公開されるよりも前の話だった…。
そしてこの morphing を作るためのコードも gist で公開されている。
読んでみると、2 つの noise の間の値を得る方法として slerp という関数が使われている。
for i, t in enumerate(np.linspace(0, 1, num_steps)): init = slerp(float(t), init1, init2)
この定義は以下のようになっている。
def slerp(t, v0, v1, DOT_THRESHOLD=0.9995): """ helper function to spherically interpolate two arrays v1 v2 """ if not isinstance(v0, np.ndarray): inputs_are_torch = True input_device = v0.device v0 = v0.cpu().numpy() v1 = v1.cpu().numpy() dot = np.sum(v0 * v1 / (np.linalg.norm(v0) * np.linalg.norm(v1))) if np.abs(dot) > DOT_THRESHOLD: v2 = (1 - t) * v0 + t * v1 else: theta_0 = np.arccos(dot) sin_theta_0 = np.sin(theta_0) theta_t = theta_0 * t sin_theta_t = np.sin(theta_t) s0 = np.sin(theta_0 - theta_t) / sin_theta_0 s1 = sin_theta_t / sin_theta_0 v2 = s0 * v0 + s1 * v1 if inputs_are_torch: v2 = torch.from_numpy(v2).to(input_device) return v2
不勉強で知らなかったが、これは "spherical linear interpolation"、日本語では「球面線形補間」と呼ばれるのかな、という手法で、3DCGの世界などではクォータニオン(Quaternion)の補間としてよく使われていたりする、ようだ。
書かれている通り、元々はクォータニオンの補間の文脈で紹介されていたが、次元数に関係なく適用することができるということらしい。
空間上での原点から2つの点へのベクトルを考え、その2つがなす角 をドット積とノルムを使って求めることができる。
始点から終点まで、
から
へと角度を線形に変化させながら2点を結ぶ円弧上を移動させていく、という感じだろうか。
画像生成モデルでの latent space における補間としては 2016年くらいには提案されていたようだ。 そういえば GAN で遊んでいたときにちょっとそういう話題を聞いたことがあったような気もする…。
しかしこれによって Gaussian noise として分散を保ったまま変化させられる、ことになるのか…? 数学的なことはちょっとよく分からない。 まぁ球面上を角度だけ変えて動いていると考えればノルムが変化しないから大丈夫なのかな??くらいの感覚でしかない…。
実際にこれを使って補間していったときにどのような変化になるか、前回の記事で書いていた sqrt を使うものと上述の slerp を使うもので ランダムな2点を繋ぐ軌跡を見てみた。2次元、3次元 空間上でそれぞれプロットすると以下のような違いがあった。
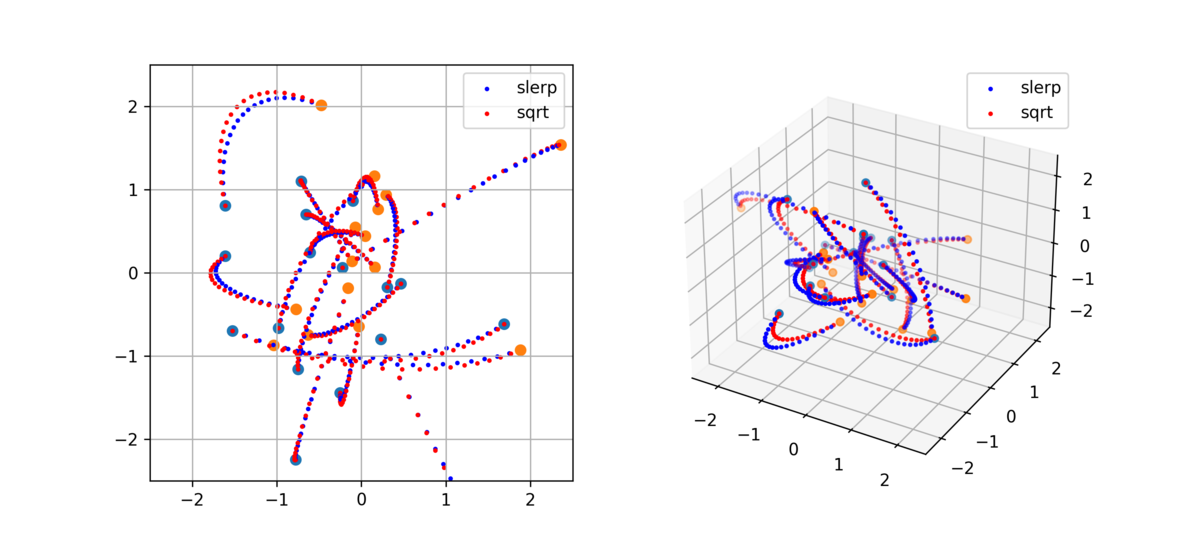
間隔が異なるだけでなく、明らかに軌道も異なるところを通るようになるようだ。
実装
引用したコードでも良いが、自分でもPyTorch前提で Slerp を書いてみる。 NumPy への変換はしなくても計算できそうだった。
def myslerp( t: float, v0: torch.Tensor, v1: torch.Tensor, DOT_THRESHOLD: float = 0.9995 ) -> torch.Tensor: u0 = v0 / v0.norm() u1 = v1 / v1.norm() dot = (u0 * u1).sum() if dot.abs() > DOT_THRESHOLD: return (1 - t) * v0 + t * v1 omega = dot.acos() return (((1.0 - t) * omega).sin() * v0 + (t * omega).sin() * v1) / omega.sin()
前述の数式の定義通りに実装するだけではあるが、やはり特別な場合に注意する必要はある。2点の原点からの方向がまったく同じか、もしくは正反対の方向のとき、理論上では単位ベクトルのドット積は 1 や -1 になる。
が、float値の多次元配列で計算してみると 多少の誤差が生じることがある。
for _ in range(10): v0 = np.random.normal([1, 4, 64, 64]) v1 = 1.0 * v0 print((v0 * v1 / (np.linalg.norm(v0) * np.linalg.norm(v1))).sum())
0.9999999999999997 1.0 1.0 0.9999999999999998 0.9999999999999999 1.0 1.0 0.9999999999999998 1.0 1.0000000000000002
for _ in range(10): v0 = np.random.normal([1, 4, 64, 64]) v1 = -1.0 * v0 print((v0 * v1 / (np.linalg.norm(v0) * np.linalg.norm(v1))).sum())
-1.0000000000000004 -1.0 -0.9999999999999998 -1.0 -1.0 -1.0 -0.9999999999999999 -1.0 -1.0000000000000002 -1.0
slerp では このドット積の値から arccos() で角度を求める必要があるが、例えば np.arccos() は 引数が -1.0 と 1.0 の間に収まっていない場合に nan を返すことになってしまう。
また、後でこの角度の sin() で割る処理があるので、ドット積が 1.0 で返せていたとしてもその後の計算で今度は inf が出てきたりする。
ので、こういうケースでは球面ではなく普通に線形で繋いでしまった方が良いだろうね、ということで DOT_THRESHOLD というものが使われて処理を分岐させているようだ。
※追記
指摘いただいたが、まったく同じ向きのときはともかく 正反対の方向の場合は線形補間が正しいとは限らない。
例えば2次元において (1, 0) と (-1, 0) を補間する場合は原点を通らず (0, 1) もしくは (0, -1) を通る円軌道になった方が良かったり 3次元の球でいうと北極と南極を繋ぐのは赤道上を通る球面軌道であって欲しい、など。
これは2点のどちらかを適度にブレさせれば算出できる場合もあるかもしれないし、上記のように明らかに通るべき点があればまず両点からそこにまず補間してやるなど、色々な考え方がありそう。これもまた用途や場合によると思われる。
今回の Stable Diffusion で使っている乱数においては正反対向きはまず有り得ないものと思ってよさそうだ。
この小数点誤差がどれくらいになるのかは、要素数だったり 計算の順番だったり numpy で計算するか torch で計算するか などによっても変わってくるようだ。
どれくらいの値になったら線形と見做すか、の閾値(上述では 0.9995)は場合によると思われる。
少なくとも Stable Diffusion で使う [4, 64, 64] の shape で torch.randn() で生成される乱数同士の場合は、通常はドット積は 0.1 にすら届くことがまずないので、極端な話ではそれくらい低くても問題なさそうではある。
morphing の2点間で同一の noise を使う可能性がない、という前提であれば分岐なくしても問題ないくらい。
比較
で、実際に slerp を使うように変更すると morphing はどう変化するのか。
以前に載せた anime girl での morphing の slerp 版を作ってみた。
slerp版 pic.twitter.com/wUXuBWHMKc
— すぎゃーん💯 (@sugyan) September 9, 2022
並べて比較
— すぎゃーん💯 (@sugyan) September 9, 2022
ちょっと変化のタイミングが変わったかな…? という程度で 大きな差は感じられない。
考察
結局のところ、Stable Diffusion においては Gaussian noise である限り何らかの画像を生成できるようになっているし、指定の2点の間をどう遷移しようと違いはないのかもしれない。
ただ slerp は線形に角度変化していくという観点でも、その遷移の移動量としてはより安定した変化が期待できるかな、という気はする。
むしろ前回の記事の手法が適当に思い付きでやった割にはそこそこ近いものが出来ていたのすごかったのでは…? というくらい。
また、今回は Gaussian noise 間でということを考えていたが slerp の手法自体は別にどこでも使えるものだとは思うので知っておいて損はないはず。また StyleGAN とかで遊ぶことがあったらそこでも使ってみても良さそう。
あと、prompt の embedding 結果に対する morphing でも slerp を使うことはできるはず、だが どうなんだろう。実験してみていないけど、A から B を遷移するのに まったく無関係な C を通過することになってしまったり 余計な変化が増えてしまうだけのような気もするので、こちらは線形に最短距離で遷移して刻み幅だけ調整するくらいが良いのではないかな、と思っている。実際にはやはりどちらでも大して変わらないかもしれないし prompt 次第かもしれない。試行錯誤するときの選択肢として持っておくと良さそうではある。