Claude Codeには OpenTelemetry (OTel) のサポートがある。
これを使ってログやメトリクスを収集し、さくらのクラウドの「モニタリングスイート」に送信する試みをした。
Claude CodeのOpenTelemetry設定
ほぼすべてのことがここに書いてある。
docs.anthropic.com
最も簡単には、以下の設定を .claude/settings.local.json などに書けば確認できる。
{
"env": {
"CLAUDE_CODE_ENABLE_TELEMETRY": "1",
"OTEL_LOGS_EXPORTER": "console",
"OTEL_METRICS_EXPORTER": "console"
}
}
通常の入出力の他に様々な情報がターミナルに現れるようになる。
otel-collectorで受ける
console出力ではなく、外部システムへの送信を目的としてOpenTelemetry Collectorにデータを流すようにしてみる。
{
"env": {
"CLAUDE_CODE_ENABLE_TELEMETRY": "1",
"OTEL_LOGS_EXPORTER": "otlp",
"OTEL_METRICS_EXPORTER": "otlp",
"OTEL_EXPORTER_OTLP_PROTOCOL": "grpc"
}
}
これにより、ログ・メトリクスそれぞれが OTEL_EXPORTER_OTLP_ENDPOINT (デフォルトで http://localhost:4317) に対し grpc で送信されることになる。
これを受け取るOpenTelemetry collectorには、後述する「モニタリングスイート」への中継を前提として以下のものを使用する。
github.com
必要最低限の機能は十分に揃っているはず。ビルド済みバイナリをダウンロードするなりdockerで起動するなり自前でビルドするなりして、repositoryに含まれている config.yaml を使って起動するだけでまずはotel-collectorの出力としてデバッグログが流れるのを確認できる。
./sacloud-otel-collector --config=./config.yaml
verbosity を detailed にするとより詳細な内容を見ることができる。
exporters:
debug:
verbosity: detailed
ログ:
2025-06-30T12:04:04.885+0900 info ResourceLog #0
Resource SchemaURL:
Resource attributes:
-> service.name: Str(claude-code)
-> service.version: Str(1.0.35)
ScopeLogs #0
ScopeLogs SchemaURL:
InstrumentationScope com.anthropic.claude_code.events 1.0.35
LogRecord #0
ObservedTimestamp: 2025-06-30 03:04:03.135 +0000 UTC
Timestamp: 2025-06-30 03:04:03.135 +0000 UTC
SeverityText:
SeverityNumber: Unspecified(0)
Body: Str(claude_code.user_prompt)
Attributes:
-> user.id: Str(***)
-> session.id: Str(c1acf7b7-d1b2-497b-9512-d8b2728259c4)
-> organization.id: Str(***)
-> user.email: Str(***@gmail.com)
-> user.account_uuid: Str(***)
-> terminal.type: Str(tmux)
-> event.name: Str(user_prompt)
-> event.timestamp: Str(2025-06-30T03:04:03.135Z)
-> prompt_length: Str(5)
-> prompt: Str(<REDACTED>)
Trace ID:
Span ID:
Flags: 0
{"otelcol.component.id": "debug", "otelcol.component.kind": "exporter", "otelcol.signal": "logs"}
メトリクス:
2025-06-30T12:01:56.754+0900 info ResourceMetrics #0
Resource SchemaURL:
Resource attributes:
-> service.name: Str(claude-code)
-> service.version: Str(1.0.35)
ScopeMetrics #0
ScopeMetrics SchemaURL:
InstrumentationScope com.anthropic.claude_code 1.0.35
Metric #0
Descriptor:
-> Name: claude_code.session.count
-> Description: Count of CLI sessions started
-> Unit:
-> DataType: Sum
-> IsMonotonic: true
-> AggregationTemporality: Delta
NumberDataPoints #0
Data point attributes:
-> user.id: Str(***)
-> session.id: Str(5d1084d1-f6f1-4feb-b5fc-4081104e9d6e)
-> organization.id: Str(***)
-> user.email: Str(***@gmail.com)
-> user.account_uuid: Str(***)
-> terminal.type: Str(tmux)
StartTimestamp: 2025-06-30 03:01:46.884 +0000 UTC
Timestamp: 2025-06-30 03:01:56.662 +0000 UTC
Value: 1.000000
{"otelcol.component.id": "debug", "otelcol.component.kind": "exporter", "otelcol.signal": "metrics"}
ここで注目すべきところは
- ログは
Body に claude_code.user_prompt といったevent名だけが入り、その他の情報は Attributes に含まれる
- promptの内容は
<REDACTED> になっている
- メトリクスは
AggregationTemporality: Delta で送られる
というところ。
otel-collectorからモニタリングスイートへ送る
ここからモニタリングスイートの話。「モニタリングスイート」のスイートは「スイートプリキュア♪」のスイートと同じスイートです。
manual.sakura.ad.jp
上記マニュアルにある通り、さくらのクラウド「モニタリングスイート」では、少なくとも2025年6月現在では対応プロトコルは
- メトリクス: Prometheus Remote Write
- ログ: OpenTelemetry Protocol (OTLP/HTTP)
となっている。
上述のotel-collectorからそれぞれ対応したexporterを設定することで、それぞれ送信できる。
コントロールパネル上でそれぞれ「ログストレージ」「メトリクスストレージ」を作成する。
各ストレージで対応するアクセスキーを作成。
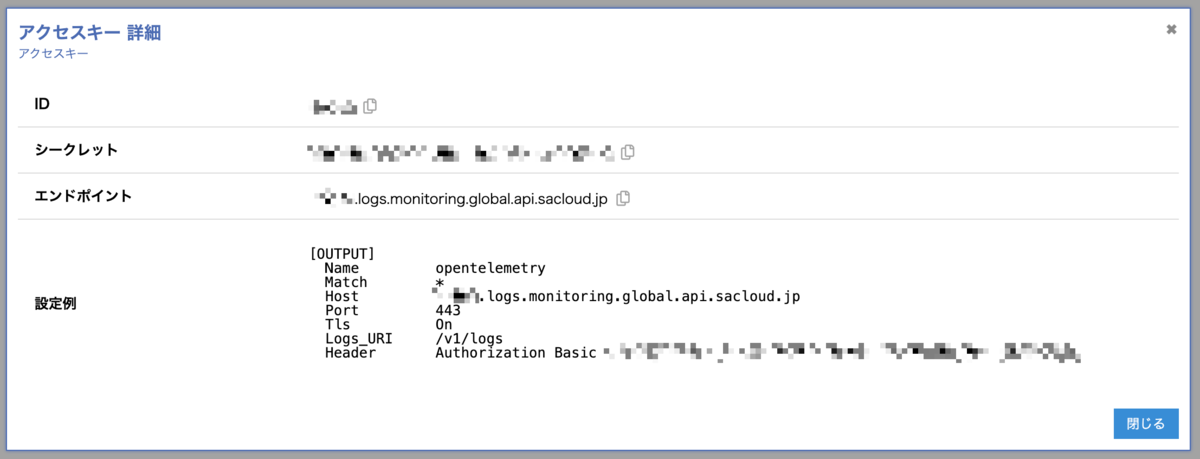
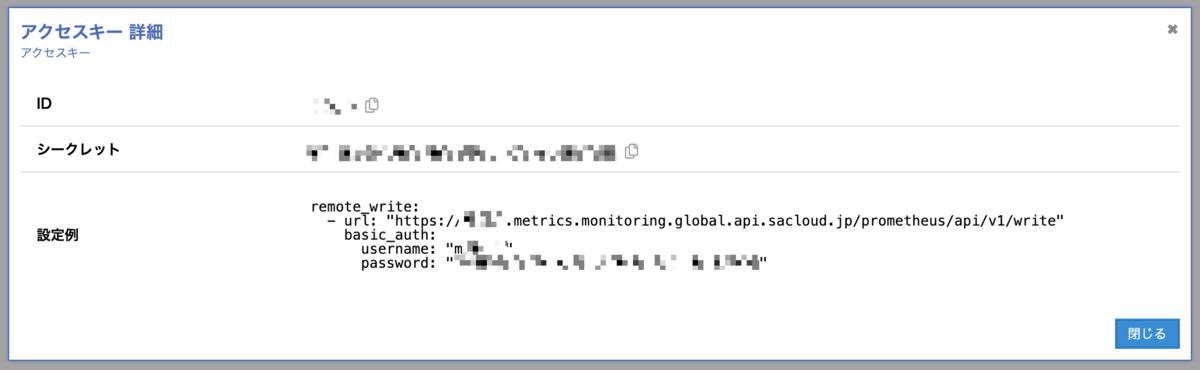
これらで得たエンドポイントとBasic認証ヘッダを使って、以下のような感じで設定していく。
メトリクスに関しては自分で usernameとpasswordからbase64エンコードしてヘッダの値を作る必要がある…。
$ echo -n "m123456:12345678-1234-5678-9abc-123456789abc" | base64
bTEyMzQ1NjoxMjM0NTY3OC0xMjM0LTU2NzgtOWFiYy0xMjM0NTY3ODlhYmM=
exportersを追加した config.yaml は以下のようになる:
exporters:
debug:
verbosity: detailed
prometheusremotewrite:
endpoint: https://************.metrics.monitoring.global.api.sacloud.jp/prometheus/api/v1/write
headers:
Authorization: Basic **********************************************************==
otlphttp:
endpoint: https://************.logs.monitoring.global.api.sacloud.jp
headers:
Authorization: Basic ********************************************************
service:
pipelines:
metrics:
receivers: [otlp]
processors: [batch]
exporters: [debug, prometheusremotewrite]
logs:
receivers: [otlp]
processors: [batch]
exporters: [debug, otlphttp]
メトリクスの設定
上記の基本設定だけでは、メトリクスは正常に送信されない。DEBUGログを出力するようにすると以下のようなエラー文言が出る。
service:
telemetry:
logs:
level: DEBUG
{"otelcol.component.id": "debug", "otelcol.component.kind": "exporter", "otelcol.signal": "metrics"}
2025-06-30T23:38:39.874+0900 debug prometheusremotewriteexporter@v0.125.0/exporter.go:219 failed to translate metrics, exporting remaining metrics {"otelcol.component.id": "prometheusremotewrite", "otelcol.component.kind": "exporter", "otelcol.signal": "metrics", "error": "invalid temporality and type combination for metric \"claude_code.session.count\"", "translated": 1}
先述の通り、Claude Codeからは AggregationTemporality: Delta で送信されるが、これは prometheusremotewrite exporterでは扱えない、とのこと。
これに対応するための一つの方法として、 deltatocumulative processorが使用できる。
processors:
batch:
timeout: 1s
send_batch_size: 1024
deltatocumulative: {}
service:
pipelines:
metrics:
receivers: [otlp]
processors: [batch, deltatocumulative]
exporters: [debug, prometheusremotewrite]
こうすることで、otel-collector側で累計値を保持して処理してcumulativeの値で書き込んでくれるようになる。
または、Claude Code側で以下の環境変数を設定しておけば、processorは使わなくてもClaude Code側で毎sessionでの累積値を送信してくれるようにはなる。
{
"env": {
"OTEL_EXPORTER_OTLP_METRICS_TEMPORALITY_PREFERENCE": "cumulative"
}
}
ログの設定
ログは特別な設定なしでも一応送信はできるが、そのままではイベント名しか記録されず、情報量が極めて乏しい。
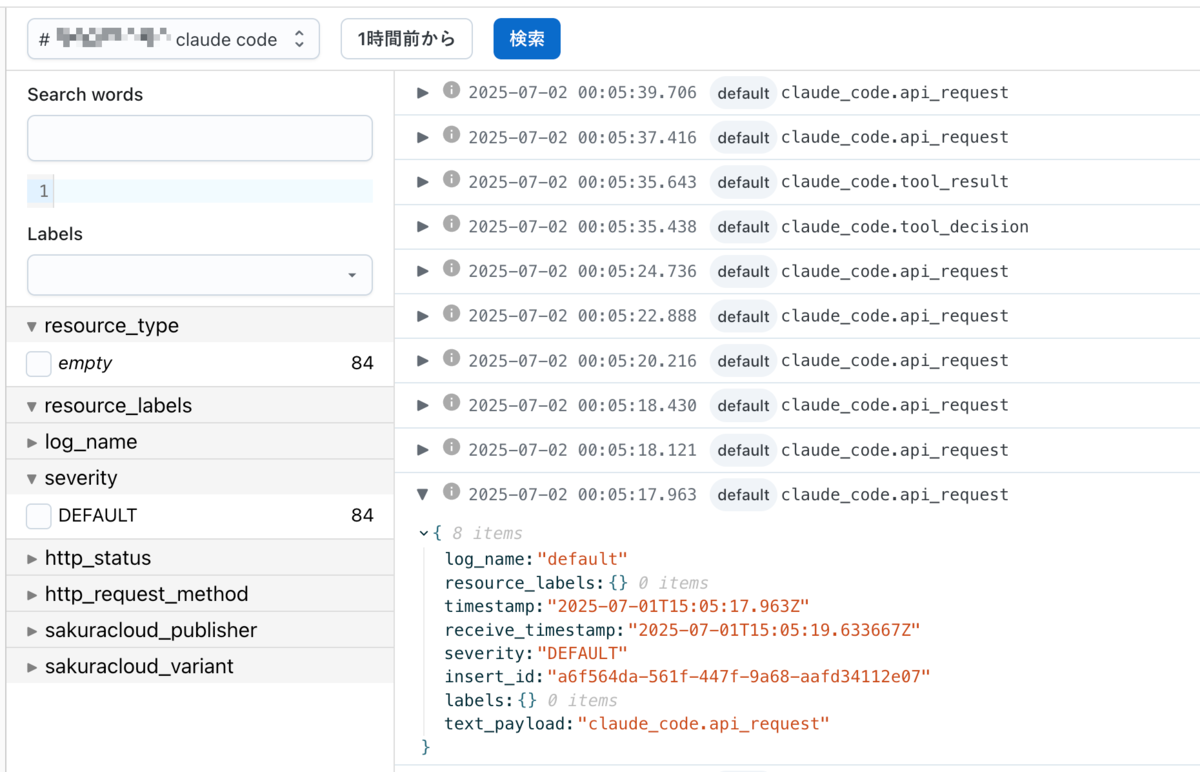
debug 出力で見た通り、多くの情報は Attributes の中に含まれていて、モニタリングスイートにはこれらの情報を Body に載せる必要がありそう。
ここでは transform processorを使う。
processors:
transform/add_attrs_into_body:
log_statements:
- 'set(log.body, {"message": log.body})'
- merge_maps(log.body, log.attributes, "upsert")
- set(log.attributes, {})
service:
pipelines:
logs:
receivers: [otlp]
processors: [batch, transform/add_attrs_into_body]
exporters: [otlphttp]
log.body を Map として持つようにし、元々入っていた Str のBodyは "message" というフィールドで持つよう変更する。そしてすべての log.attributes をその log.body にmergeする。元々の log.attributes は含めていても無駄になるだけなので空にしてしまう。
こうしてやることで、 json_payload として Attributes に含まれていた情報をモニタリングスイートで閲覧することができるようになる。
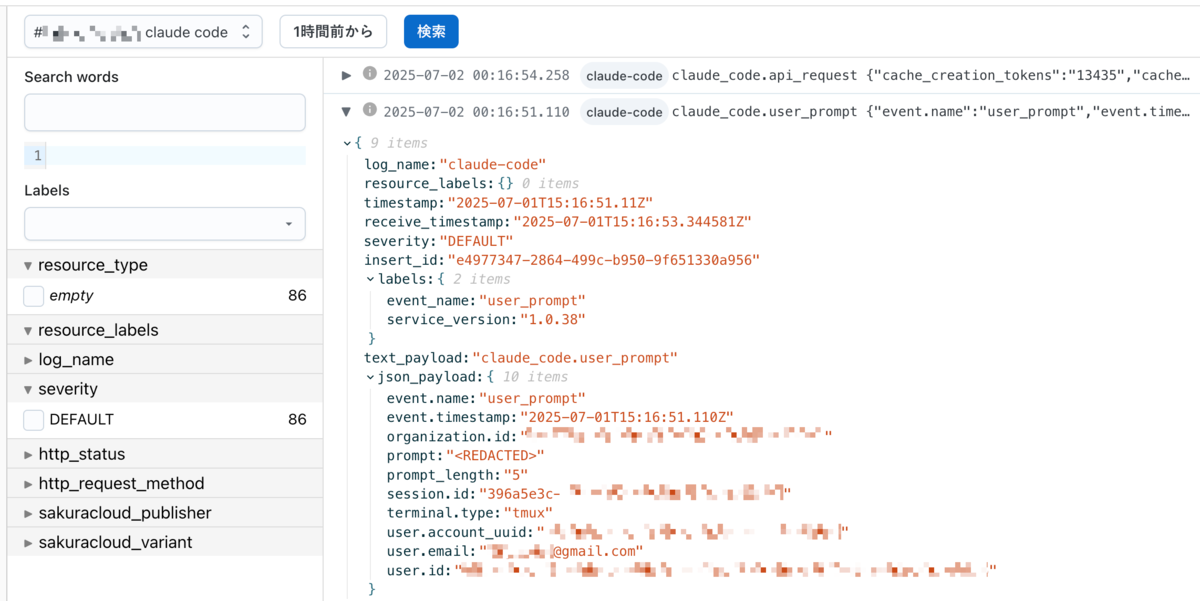
user_prompt の prompt はデフォルトで <REDACTED> と記録されるが、これはClaude Code側の OTEL_LOG_USER_PROMPTS の設定で変えることはできる。
{
"env": {
"CLAUDE_CODE_ENABLE_TELEMETRY": "1",
"OTEL_EXPORTER_OTLP_PROTOCOL": "grpc",
"OTEL_LOGS_EXPORTER": "otlp",
"OTEL_LOG_USER_PROMPTS": 1
}
}
さらにHooksも
Claude Codeの最近の更新(v1.0.38以降)では、各イベント時にカスタム処理を実行できるHooks機能が追加されている。
これらをログとして取得して送信したい場合は以下のようなスクリプトを用意しておくと良さそう。
HOOK_NAME="$1"
OTEL_ENDPOINT="${OTEL_ENDPOINT:-http://localhost:4318/v1/logs}"
if [ -z "$HOOK_NAME" ]; then
echo "Usage: $0 <hook_name>" >&2
exit 1
fi
jq -n --argjson body "$(cat)" --arg hook "$HOOK_NAME" '{
resourceLogs: [{
resource: {attributes: [{key: "service.name", value: {stringValue: "log-sender"}}]},
scopeLogs: [{
logRecords: [{
timeUnixNano: (now * 1000000000 | tostring),
body: {kvlistValue: {values: ([$body | to_entries[] | {key: .key, value: {stringValue: (.value | tostring)}}] + [{key: "hook.event", value: {stringValue: $hook}}])}},
attributes: []
}]
}]
}]
}' | curl -X POST \
-H "Content-Type: application/json" \
-d @- \
"$OTEL_ENDPOINT"
otel-collector では receivers で http も指定してあればこのように curl でPOSTすることもできる。
あとは、Claude Code側で hooks 設定をそれぞれ指定する。
{
"env": { ... },
"hooks": {
"PreToolUse": [
{
"matcher": "",
"hooks": [ { "type": "command", "command": "./otel-log-sender.sh PreToolUse" } ]
}
],
"PostToolUse": [
{
"matcher": "",
"hooks": [ { "type": "command", "command": "./otel-log-sender.sh PostToolUse" } ]
}
],
"Notification": [
{
"matcher": "",
"hooks": [ { "type": "command", "command": "./otel-log-sender.sh Notification" } ]
}
],
"Stop": [
{
"matcher": "",
"hooks": [ { "type": "command", "command": "./otel-log-sender.sh Stop" } ]
}
]
}
}
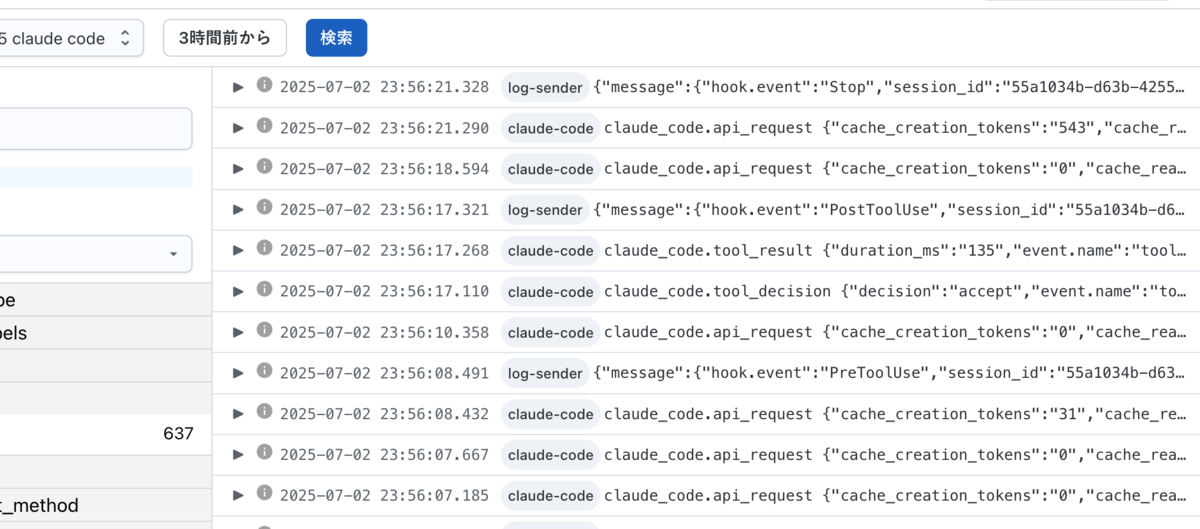
こうして様々な情報をログとして残しておくことができるようになる。
メトリクス可視化
メトリクスが正常に保存されていれば、モニタリングスイートの可視化機能を使ってダッシュボードを作成できる。
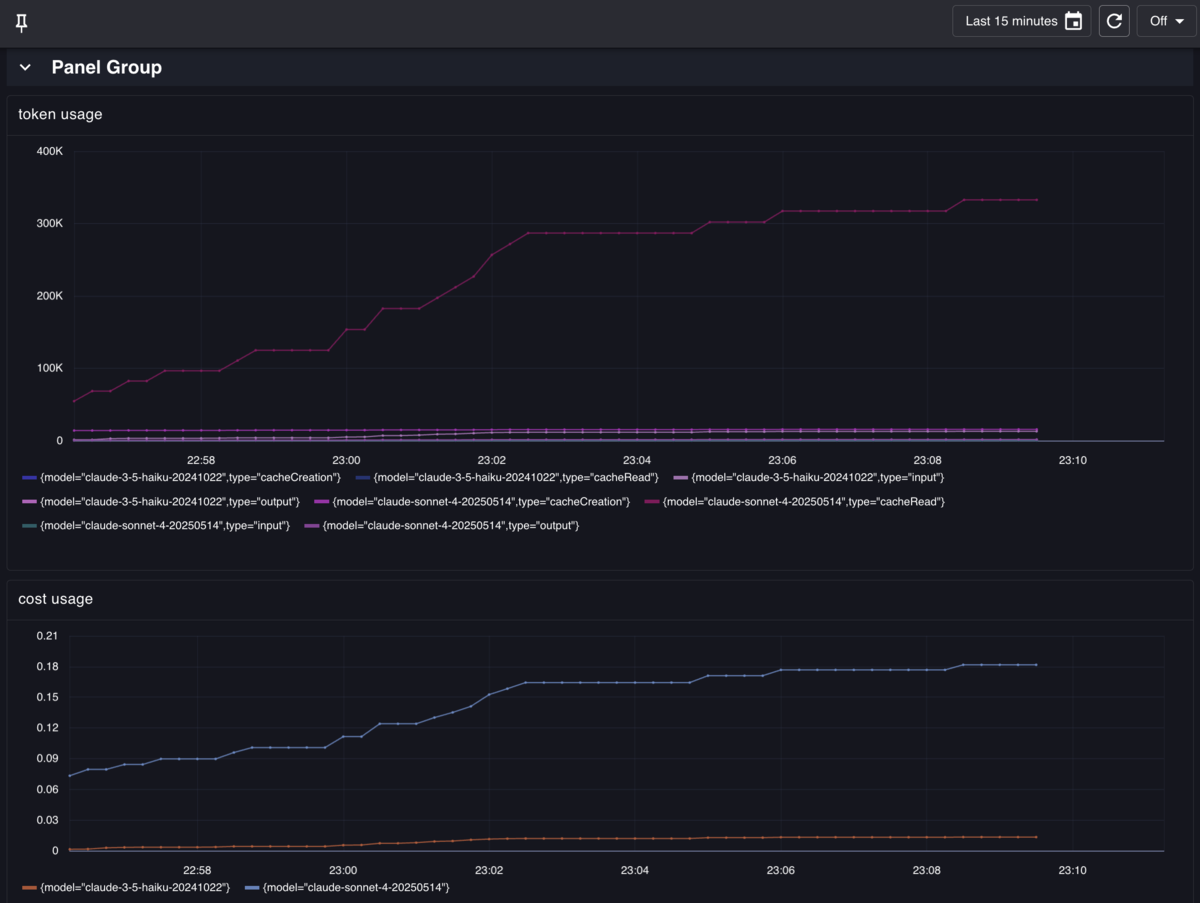
クエリ例:
sum(claude_code_token_usage_tokens_total) by (type, model)
これらの値を使ってアラートを設定して通知送信する、といったこともできるがここでは割愛…
まとめ
Claude CodeのOpenTelemetryサポートを活用して、ログとメトリクスをさくらの「モニタリングスイート」に送信する環境を構築した。
主なポイント:
- Claude Code側でOTelの設定を行い、otel-collectorに送信
- メトリクスはDelta形式で送られるため、
deltatocumulative processorまたは累積モード設定が必要
- ログはAttributesの情報をBodyに含めるため
transform processorで変換が必要
- Hooksを活用することで独自のイベントログも収集可能
これにより、Claude Codeの使用状況を詳細に監視・分析できる環境が整った。メトリクスの可視化やアラート設定により、使用パターンの把握やトークン消費量の管理も行える。









