以前書いた、詰将棋問題生成の続き。
逆算による詰将棋の問題生成の方法自体は悪くないとして (バグによって有り得ない局面が出来上がったりしてしまったりもしたけど)、正しく詰将棋問題として成立するものが出来上がっているかどうかを検証するためのSolverが必要不可欠であり、これのパフォーマンスが生成のパフォーマンスにも影響してくる、というようなことを書いた。
実際、前回の記事のときに実装したSolverでは
- 総当たり的に探索するのは3〜5手が限界
- 詰将棋のルールに則る動きに限定しても、有り得る局面は指数関数的に増加する
- 合駒が絡む問題に対して正しく解が導けないことがある
- 先の展開まで読まないと無駄な合駒かどうかの判定ができない
といった問題があった。
df-pnアルゴリズムによる探索
2002年の論文「df-pn アルゴリズムの詰将棋を解くプログラムへの応用」がとても有名なもののようだ。
ざっくり、概要というか考え方について書いてみる
AND/OR Tree
まず、指し手とそれによる局面の変化を "AND/OR Tree" で考える。
例えば前回の記事で作成した問題に対しては、2手目までで以下のようなパターンが考えられる。
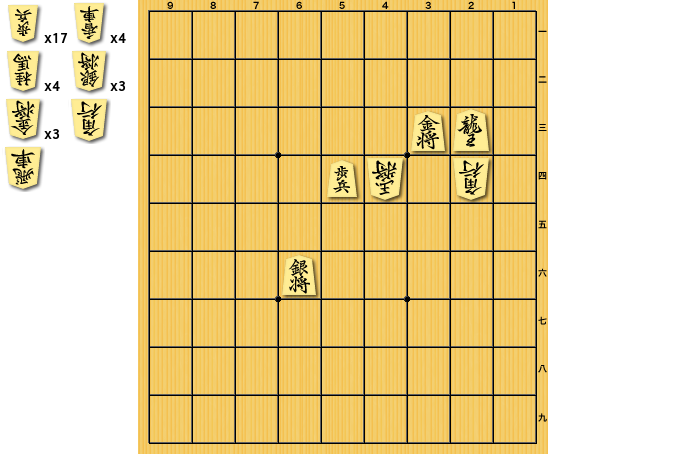
├─┬ ▲4三金 │ ├── △3五玉 │ ├── △4五玉 │ └── △5四玉 ├─┬ ▲3四金 │ ├── △4五玉 │ └── △5四玉 ├── ▲3四竜 ├─┬ ▲2四竜 │ ├── △4五玉 │ ├── △3四歩 │ ├── △3四香 │ ├── △3四桂 │ ├── △3四銀 │ ├── △3四金 │ ├── △3四角 │ └── △3四飛 └─┬ ▲5五銀 ├── △同玉 ├── △3五玉 └── △4五玉
「詰み」をTrue、「不詰」をFalseと考えると、攻方手番の局面は「OR節点」、玉方手番による局面は「AND節点」となる。そして深さが変わるごとに「OR節点」⇔「AND節点」を交互に繰り返すことになる。
すなわち、上図での根(攻方手番)では「どれか1つの子節点でもTrueになればTrue、すべての子節点がFalseならばFalse」であり、その子となる深さ1の節点(玉方手番)では「すべての子節点がTrueになればTrueになり、どれか1つでも子節点がFalseならFalse」となる。
これはまさに詰将棋のルール通りで「どうやっても詰むことが出来なくなったら不詰」「どう応じられても詰ますことが出来れば詰み」といったものを 論理演算のAND/ORで表現している。
なので、最終的に上述のAND/OR Treeの根がTrueであることを証明できれば、それが詰将棋問題の解答に繋がる、ということになる。
単純に考えると すべての節点をどんどん掘っていって その節点が葉となったら(つまりもう子節点が作れない)、動かせる有効な手が存在しないということなので それが攻方手番ならTrue、玉方手番ならFalseである、と確定できる。
しかし全節点を探索していくとなるとその探索空間は非常に膨大なものになり、特に不詰の場合は玉がどこまでも逃げていく局面があったりして、大変な計算時間になってしまう。
AND/OR Treeは上記の性質上、どこか1つの節点の真偽値が確定するとその時点で親節点の真偽値も確定し 他の兄弟節点について調べる必要がなくなる場合もあるので、探索の方法次第では効率的に根の真偽値を確定させることができる。根の真偽値を確定させるだけなら、すべての節点についてTrueかFalseであるかをハッキリさせる必要がなく、不確定の節点があっても構わない。
上の例で示した問題の場合、1手詰で▲3四竜の場合にもう玉方の応手が無く「詰み (True)」になっているので 他の手から伸びていく深さ2以上の節点は調べるまでもなく「詰み」であることを言える。
df-pnアルゴリズム
df-pnアルゴリズムでは、このAND/OR Treeを効率良く探索するために、「証明数 (proof number)」「反証数 (disproof number)」という概念を用いる。簡単に言うと「その節点がTrueであることを証明するためにTrueであることを証明しないといけない節点の数」、またはその逆、という感じで、詰将棋でいうと「この手を指して詰むことを証明するためには、玉方の応手この手とこの手が考えられて…これらの局面でも詰むことを証明できなければ…」というパターン数のようなものになる。
これらの値を各節点で計算し、より値の小さいもの(その局面の真偽値を確定させるために証明すべき節点の数が少ないもの)を優先的に深さ優先で探索していく。これが depth first proof number (df-pn) アルゴリズムの基本的な考え方、のようだ。 実際に詰将棋を解くときも、まずは応手が限られる手から考えたり それに対する応手も最悪のパターンを優先的に考えたりすると思うし、直感的に近いものはあるんじゃないだろうか。
ポイントとしては、必ずしもすべて節点の真偽値を確定させる必要はなく、「詰み (True)」「不詰 (False)」「未知 (Unknown)」の3つの状態が許されると考えて木を探索していき、その上で簡単に確定させることが出来そうな未知節点から優先的にさらに深く探索していく、というところ。
このアルゴリズムに用いられている手法により、探索の結果として各節点の証明数・反証数が更新されていく。証明数が∞になると「この節点がTrueであると証明するために証明すべき節点が無限にある → つまりこの節点はFalse」、反証数の場合はその逆で、これらの値によって節点の真偽値を確定させることが出来る。
論文内では、単純にそれだけではなく ハッシュ(というかハッシュテーブル、辞書?)を用いて、同一局面が現れる場合の無駄な探索を減らし、それらに加えて局面がループするときに起きるGHI (Graph History Interaction)問題に対する対処などの工夫を入れている。
実装
論文の付録に疑似コードが載っているので、これをそのままコードに落とし込めば ほぼ問題ない、はず (全然簡単には出来なかったけど、、)。
先行例としては以下のものなどを参考にさせていただきました。
- https://github.com/makudenki/libshogi/blob/master/example/dfpn/Main.cpp
- https://github.com/TadaoYamaoka/DeepLearningShogi/blob/master/usi/DfPn.cpp
自分はGoで将棋プログラムを書いていたのでGoで。
df-pn Solverの特徴・制約
ということで、df-pn Solverを実装することで詰将棋の問題を正確に速く解くことが出来るように… と言いたいところだけど、これですべて解決というわけではない。
df-pnアルゴリズムによって解くのはあくまでも『その局面が「詰み」か「不詰」かを判定し、その証明ができる』だけであって、『詰将棋の問題に対する正解を導ける』わけではない。
例えば、以下のような問題。
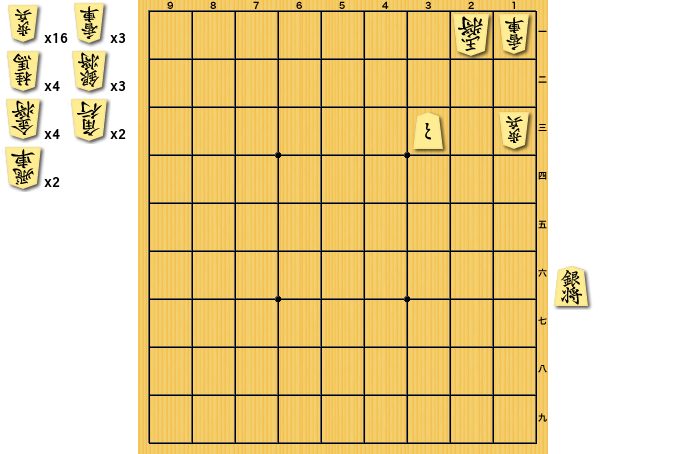
これを自作のdf-pn Solverを使って解くと、以下のようにAND/OR Treeと各節点の真偽値が得られる。
├─┬ ▲3二と (?)
│ ├── ...
│ └── ...
├─┬ ▲2二と (?)
│ └── ...
├─┬ ▲2二銀 (?)
│ └── ...
├─┬ ▲1二銀 (?)
│ ├── ...
│ ├── ...
│ └── ...
└─┬ ▲3二銀 (T)
└─┬ △1二玉 (T)
├── ▲2一銀 (?)
├─┬ ▲2三銀成 (T)
│ └─┬ △2一玉 (T)
│ ├── ▲3二と (T)
│ ├── ▲2二と (?)
│ ├── ▲2二成銀 (?)
│ ├── ▲1二成銀 (?)
│ └── ▲3二成銀 (?)
├── ▲2三銀 (?)
├── ▲2三と (?)
└── ▲2二と (?)
()内に書いてあるのが?は真偽未確定、TはTrue、FはFalseを表す、とする。
...で省略しているけど実際にはもう少し他の1手目に対しても深く探索されている。
結果としてこの得られた木のTrue節点を辿っていくことで「▲3二銀 △1二玉 ▲2三銀成 △2一玉 ▲3二と」という5手の詰み手順を得ることができる。
これは確かに詰んでいるのだけど、「正解ではない」。
実際は「▲3二銀 △1二玉 ▲2三と」までの3手詰で、これが最短の正解となる。
df-pnアルゴリズムは性質上、各節点の証明数・反証数を計算し対象となる節点の値が閾値を超えた時点で探索を終了する。つまり多くの場合は根の真偽値が確定した時点で終了となり、当然ながら現れている全部の節点について探索を行うわけではない。
ので、このように深さ優先で探索した結果、3手目の▲2三との節点を探索する前に▲2三銀成の節点から詰みを見つけてしまい、それで終了してしまう、ということがある。
おそらく指し将棋プログラムでの思考ルーチンとして組み込むぶんにはそれほど問題なく使えると思うのだけど(指し将棋の目的は通常「勝つこと」なので 最短の手順である必要はない)、詰将棋においては「最短で最善の手順で詰む(玉方も最長になるよう最善の手で応じる)」ということを踏まえて解を導かなければならない。 単純に探索終了したら正解が導ける、というものでもないようだ。
また、「不詰」の証明にも少し弱いようで(これは自分の実装のミスか何かなのかもしれないけど)、例えば以下のような局面を解かせようとすると、いつまでも計算が終わらない。
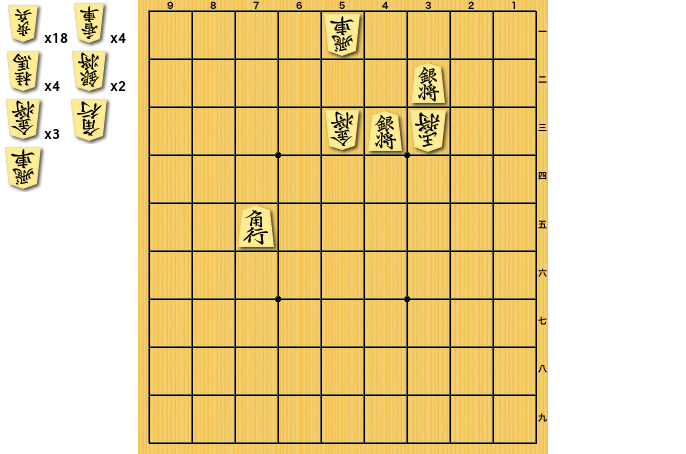
df-pnアルゴリズムは各節点での証明数・反証数が閾値を超えると一度探索を止めて その閾値以下の別の節点の探索に移り また別のところで閾値が上がるとそこに戻ってきたりする、という仕組みになっているようなのだけど、どうも上記の局面などの場合 別々の節点から辿り着く複数の節点がそれぞれ閾値をお互いに上げていってしまい どちらも譲らずどこまでも証明数やその閾値が増加しつづけていって止まらなくなってしまうようだ。
最善解の導出
…と、ここまで書いてきたところで ここからが本題。
df-pn Solverは完璧に答えを出すことが出来るものではないけど、効率的に探索を行い特定の問題を解くのには利用できるので、これを応用することで「詰将棋の解答プログラム」を作ることを考えた。
別解を探す
先述のように、実際は3手で詰めるものに対して5手で詰む解を導いてしまう、といったことが起きる。 これを回避するためには「実際に他の手でもっと短く詰むことが出来ないかを調べる」ということになる。
単純には、探索が終了してもまだ真偽値が確定していない節点に対して再度Solverにかけて探索していく、という手法をとることになるけど、結局それだと総当たりで調べるのとほぼ変わらなくて効率が良くない。
一つ大事なのは、これを探し始める時点で1つの正解候補となる解答が導出できているので、「それより短い手順で解ける手はないか」だけを探索すれば良いことになる。 既に導いている解より長くなる詰み手順を見つけても無意味なので どこまでも深く探索する必要はなく、ある閾値以上の深さに辿り着いた時点で「これは不詰」と扱って探索を打ち切ってしまっても良い。
既に見つけている正解手順以外の手を探索した結果 より短い詰み手順を見つけることが出来たら、正解候補を更新して またもっと短い手順が無いか探索する。こうしていくことで探索の深さ上限を小さくしながらすべての未確定節点の真偽値を確かめていける。
また大事なのは探索対象の未知節点を選ぶ順番で、例えば1手目から正解候補と違う節点を調べようとしても大抵は不詰なので(いわゆる完全作の場合、正解手順は1つのみで最終手以外に余詰は存在しない)、探索空間が大きく無駄に時間がかかってしまう。 先にもっと短い解候補が発見できていれば探索深さの上限を下げられるので効率が良くなる。
なので基本的には深さ優先で、その時点で発見できている正解候補の手順の周辺の未知節点から探索していくのが効率が良い。7手の詰みが見つかっているのならその手順を辿りつつ別の5手目、別の3手目、という順番で選択して探索していくと より速く短い解候補が発見できる。はず。 その結果として例えば3手で詰む手順が発見できれば、1手目で違う手順を探索する(不詰であることを証明することになる)場合にはもう4手目以降の深さは考慮せず打ち切ることができる。
また、先述のように不詰の証明は計算が終わらない事態が起こることがある。
これについてはどうしようもなかったので、計算時に用いる∞の値をギリギリまで小さくすることで回避した。
正しく「詰み」を導くことができる場合は証明数はせいぜい数百〜千程度の値までしか上がらないので、それより少し大きな値を∞としておけば 先述のような状態になってもいずれは「証明数が∞に到達した」となり、不詰として扱うことができるようになる。
現時点で自分で試している限りでは 2^12 (= 4096) くらいの値にしていても大抵の7〜9手くらいまでは問題なく解けている。
最善経路の探索
Solverによる探索によって新規に詰みの手順が見つかるごとに、「最短・最善の解候補」を算出することになる。
解となる詰み手順は、基本的には探索後のAND/OR Treeの根からTrueの子節点を選択して葉に到達するまで下っていくことで求められる。
とはいえその経路は一意ではなく 複数の兄弟節点で詰みに繋がる場合も多い。特に玉方手番は「すべての子節点がTrueになればTrueになり、どれか1つでも子節点がFalseならFalse」というAND節点であり、どう応じられても詰むことができる ということが確定していない限りTrueにはならないので、玉方に複数の応手がある場合はすべてが詰みに繋がるようになっているはず。
ではどの経路を正解候補として選択するか。 詰将棋のルールとして「玉方は最善を尽くし、最も長く手数がかかるように逃げる」そして攻方は「最善・最短で詰ます」というのがあるので、これを満たすよう考える。
さらに駒余りも考慮して、すべての節点において
- 攻方手番で複数の選択肢がある場合は最も手数が短くなる経路
- 同手数のものが複数ある場合は駒を余らせる方を優先
- 玉方手番で複数の選択肢がある場合は最も手数が長くなる経路
- 同手数のものが複数ある場合は駒を余らせない方を優先
を選択するようにして、再帰的に求めていく。
合駒問題
このあたりで登場してくるのが「無駄合駒判定」の問題。
なかなか厄介なルールで、玉方による合駒が有効な場合と無効な場合がある。 すぐに取られて王手が続くなら無効、ということで「玉方の利きが無い位置に打つのはすべて無駄」と考えて そういう場所に合駒できない前提で解いてしまうのがラク… だと思いきや、そうとも限らなくて。 有名なのは看寿賞作品の3手詰「新たなる殺意」のような場合。
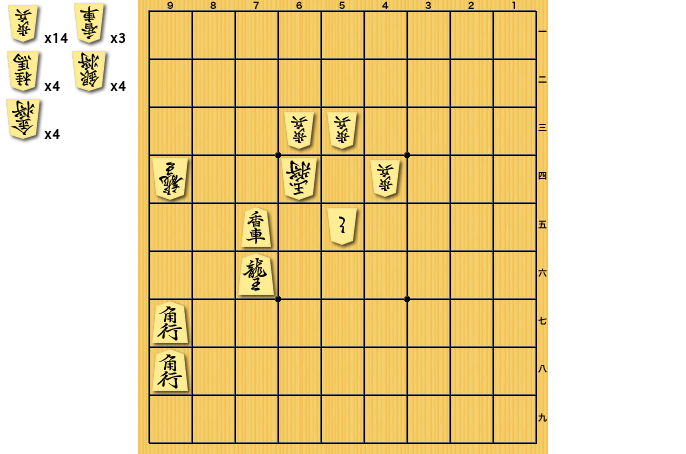
ここに▲7三香成としたときの△8六歩は玉方の利きもなく無駄…に思えるのに、▲同角により9筋が開くことによって最終的に詰みが無くなってしまう。有効な合駒となる。
こういう場合もあるので、応手の候補を考える段階ではまだ「ここには合駒できない」という明確な判断はできず、結局すべての可能性を考慮した上で「合駒で打った駒がすぐ取られて、最終的にその駒を余らせて詰ますことができる」場合は無駄合駒、と判断するしかない。
なので、AND/OR Treeの探索の時点ではとりあえず合駒も含めてすべて探索し、その上で解答候補の詰み手順を探索する段階で 合駒が無効なものであったかどうかを判断する必要がある。
再帰的に解答を探索している中で、「玉方合駒 → 攻方同取る」があった場合には最終的な駒余りを確認し、その合駒に打ったものが余る場合は解答候補から外す。このようにすることで無駄合駒の絡む問題に対しても正しく解を導けるようになる。
ただしそれはつまり、必ずしも「節点の深さ=詰み手数」にはならない、ということで、ちょっと例が見つからなかったけど「先に5手の詰みが見つかったが、実は3手の合駒利かずの詰みがある」といった場合に、先に見つかった5手を探索深さの上限値として打ち切る設定で他の手を探索すると 「連続無駄合駒により深さ7で詰むが結果的には3手の詰み手順となる」といった手順を見つけられなくなってしまう。 ので、合駒を含む経路に現れる節点は例外として上限値よりもさらに深いところまで探索する、といった処理を入れるようにした。
余詰の検出
こうしてAND/OR Treeを使った「最善解の導出」が出来ると、同じように「余詰の検出」も簡単に行うことが出来る。
詰将棋の問題生成におけるSolverの重要性は前記事に書いた通りで、生成された問題が
- 正しく意図した手数で詰ますことができる
- 駒余りが無い
- 余詰が無い
ことをチェックする必要がある。 最善解を導く過程で最短手数以内の全節点についての真偽値は確定しているはずなので、同様に根から探索しつつ「攻方に同手数で解ける複数の解が存在しないか」をチェックしていくだけ。 1手詰め以外の場合の最終手は複数あっても良いのでそこだけは許容する。
問題生成への応用
こうして、最善解・余詰をそれなりに速く正確に導くことができると 5手詰や7手詰の問題の場合でも前記事で書いたような問題生成ロジックで「正しく詰将棋の問題として成立しているか」をチェックしていくことができる。
ただしどうしても先述のように不詰の証明でループし続けたり、合駒の探索が余計な深さを必要とするなどで解答に異常に時間がかかってしまう場合がある。 なのでtimeoutを設定し、解答に一定以上の時間がかかってしまった場合はそこで「この問題は解けない」と判定して次のパターンで生成を試みるように、とした。
時間はかかるが、とりあえず前記事と同様のロジックで5手詰の問題も生成できるようになったようだ。
5手詰の問題です!
— 詰将棋BOT (@tsumeshogi_bot) February 25, 2018
正解はこちら → https://t.co/7aq06P1MW4 pic.twitter.com/qaZxku5JxZ
今後の課題や展望など
評価・解説
AND/OR Treeを丁寧に探索することで、「どれくらいのパターン数の手を考慮することでこの解答を導くことが出来たか」を測ることができる。 攻方も玉方もほぼ1手に絞られるような簡単な問題なら総節点数の少ない小さな木になるし、多くの選択肢が考えられる場合は幅の広い木になる。 この木を作る過程で考慮した節点の数を「問題の難しさの指標」として使うことができそうだ。
未知のままでも兄弟節点の真偽により親節点の真偽が確定している場合などは考慮しなくて良いので、基本的には真偽値が確定している節点の数だけを数え上げれば良いことになる。 ただし単純にそれだけを考えると、持駒に飛車角があって離れた場所にも打つことが出来る場合や 玉方が合駒する場合など(最大で7種類を合駒の候補として考えられる)に どうしても選択肢が増えるので、そういう場合には間引きするように少し調整してみている。
とりあえずはこうして得られる「スコア」を各問題の生成時に一緒に計算しておき、@tsumeshogi_botなどではそれなりにスコアの高めのものを優先的に選択して出題するようにしてみている(…つもりなんだけど、あんまりうまくいってないかも)。
問題が「良問かどうか」というのは探索量などとはまた別の評価指標もありそうなので、このへんも研究して より「良い問題」も量産できるようにしていきたいところ。
もう一つAND/OR Treeを有効利用できる点として、その木を見ることで「この手はどうして詰むか、この手だとどうして詰まないか」が説明できるようになる、というのが挙げられる。
つまり解いた問題に対して 例えばFalseの節点とその子節点を見れば「▲3二とや▲2二とには△同玉、▲2二銀には△1二玉で詰みません」、Trueの節点を辿れば「▲3二銀が正解で△1二玉の一手、これに△2三とで詰みです」という文章を、ある程度のテンプレートを用意しておけば作れる、はず。
まだ出来ていないけど、生成した問題にそれぞれこういった解説文をつけられると良さそうだな、と思っている。
計算速度
問題生成時にはランダムな詰み局面を生成してからそれを巻き戻して局面を作って それが詰将棋として成り立っているかどうかをチェックする…、というのを繰り返していて、運次第ではあるけど それなりに時間がかかる。
現状、3手詰くらいなら数秒〜数十秒程度で生成できるが、5手詰めは相当運が良くない限りは数分〜十数分計算し続けてようやく出来上がる、といった感じになってしまっている。 生成するたびにかけるSolverが速く解いてチェックしてくれればそれだけ生成速度も上がるはずではあるのだけど、まだまだパフォーマンス不足なようだ。 1.0秒でtimeoutする設定にしているけど、それも頻繁に起きている。
先述のように、合駒が絡む場合にどうしても探索の幅・深さが深くなって計算時間がかかってしまう問題がある。 いちいちすべての合駒パターンを考慮していると膨大な計算時間になってしまうので、これは減らす必要がありそうだ。 これには引用論文にもある「優越関係の利用」が使えそうで、ある局面が詰むならそれより持駒の少ないこれらの局面も詰みである、といったことが言えるようになるので 計算量を減らすことができそうだ。
あとはまぁ 自分が書きやすく管理しやすいGoでゼロから書いてみていたけど、やはりパフォーマンスを考慮するならC++とかで良いライブラリを利用して作るのが良いのかもしれない…とか。 それで実際どれくらい速くできるのか分からないけど。
生成ロジック自体もまだ無駄な計算を減らせる部分があると思うので、じっくり見直して改善していきたい。